एबे की ज्या शर्त

चिन्ह परिपाटी (Sine convention)

अक्षीय या अनुदैर्ध्य दूरियों के लिए (For axial or longitudinal distance)

• वे सभी दूरियां जो प्रकाशीय अक्ष या इसके समान्तर मापी जाती हैं, अक्षीय या अनुदैर्ध्य दूरियां होती हैं।
• वे सभी दूरियां जो प्रकाशीय केन्द्र O से आपतित प्रकाश किरण की दिशा में मापी जाती हैं, धनात्मक ली जाती हैं तथा वे सभी दूरियां जो आपतित प्रकाश किरण की विपरीत दिशा में मापी जाती हैं, ऋणात्मक ली जाती हैं।

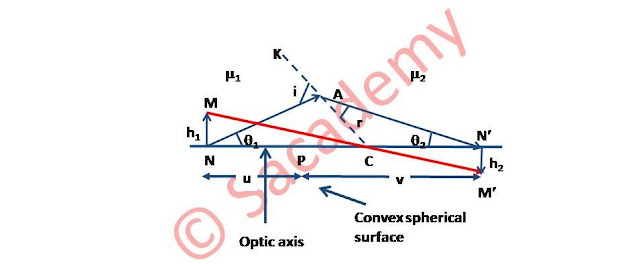
एबे की ज्या शर्त (Abbe’s sine condition)

• चिन्ह परिपाटी के उपयोग से
• h₁ तथा v धनात्मक हैं।
• h₂ तथा u ऋणात्मक हैं।
• θ₁ तथा i धनात्मक हैं एवं θ₂ ऋणात्मक है।

• यही एबे की ज्या शर्त है।
• यह सम्बन्ध θ₁ तथा θ₂ के सभी मानों के लिए मान्य है।
• इस अवस्था में अक्ष पर स्थित किसी बिन्दु N का सतह XY से अपवर्तन के पश्चात्‌ प्रतिबिम्ब N՛ बनता है।
• कोई सतह जो यह गुण दर्शाती है,  अविपथी सतह (aplanatic surface), कहलाती है। इस प्रकार की सतह का प्रयोग सूक्ष्मदर्शी के अभिदृश्यक लेन्स में किया जाता है।
• यदि अपवर्तक सतह का द्‌वारक अत्यन्त छोटा हो, तो θ₁ तथा θ₂ के मान अत्यन्त कम होंगे।

∴           sin θ₁ ≈ tan θ₁ तथा sin θ₂ ≈ tan θ₂

अतः       µ₁h₁ tan θ₁ = µ₂h₂ tan θ₂

• यह लेग्रांज समीकरण (Lagrange’s equation) है।
• साथ ही θ₁ तथा θ₂ के मान अत्यन्त अल्प होने पर tan θ₁ ≈ θ₁ तथा tan θ₂ ≈ θ₂

           µ₁h₁ θ₁ = µ₂h₂ θ₂

• यह हेल्महोल्ट्ज समीकरण (Helmholtz equation) है।