Abbe’s sine condition | Optics

Sacademy May 18, 2023 2 min read

Abbe’s sine condition

Sign convention

For axial or longitudinal distance

The distances measured along optic axis or parallel to optic axis are known as axial or longitudinal distance.
All the distances measured in the direction of incident ray from optical centre O are taken as positive, and all the distances measured in the direction opposite to the incident ray are taken as negative.

For transverse or lateral distance

All the distances measured perpendicular to the optic axis are known as transverse or lateral distances.
The transverse distances above the optic axis are taken as positive and the transverse distances below the optic axis are taken as negative.

For angles

The angles measured in anticlockwise direction with optic axis are measured as positive, and the angles measured in clockwise directions are measured as negative.
∠ θ₁ is negative, and ∠θ₂ is positive.

Note

All the longitudinal distances should be measured from optical centre, and all the lateral distances should be measured from optic axis.

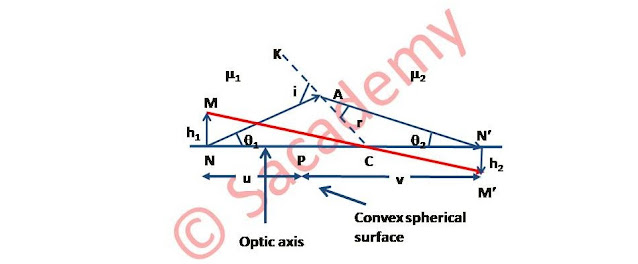
Abbe’s sine condition

By using sign convention
h₁ and v are positive.
h₂ and u are negative
θ₁ and i are positive, and θ₂ is negative.

From △CNM and △CN՛M

$\frac{N'M'}{NM}=\frac{N'C}{NC}=\frac{PN'-PC}{PN+PC}$

$or\;\;\;\;\; \frac{-h_{2}}{h_{1}}=\frac{v-R}{-u+R}$

$or\;\;\;\;\; \frac{h_{2}}{h_{1}}=\frac{v-R}{u-R}$

By using sine law in △ANC

$\frac{sin\theta _{1}}{AC}=\frac{sin\;NAC}{NC}$

$or\;\;\;\;\;\frac{sin\theta _{1}}{R}=\frac{sin(180^{\circ }-i)}{PC+PN}$

$or\;\;\;\;\;\frac{sin\theta _{1}}{R}=\frac{sin\;i}{R-u}$

By using sine law in △AN՛C

$\frac{sin\theta _{2}}{AC}=\frac{sin\;r}{CN'}$

$or\;\;\;\;\;\frac{-sin\theta _{2}}{R}=\frac{sin\;r}{v-R}\;\;\;\;\;(CN'=PN'-PC=v-R)$

$\because \;\;\;\;\;\frac{sin\theta _{1}}{R}=\frac{sin\;i}{R-u}\;\;\;\;\;and\;\;\;\;\;\frac{-sin\theta _{2}}{R}=\frac{sin\;r}{v-R}$

$\therefore \;\;\;\;\;\frac{sin\theta _{1}}{-sin\theta_{2}}=\frac{sin\;i}{sin\;r}\times \frac{v-R}{R-u}$

$or \;\;\;\;\;\frac{sin\theta _{1}}{sin\theta_{2}}=\frac{sin\;i}{sin\;r}\times \frac{v-R}{u-R}$

$or \;\;\;\;\;\frac{sin\theta _{1}}{sin\theta_{2}}=\frac{sin\;i}{sin\;r}\times \frac{h_{2}}{h_{1}}\;\;\;\;\;\left (\because \;\; \frac{h_{2}}{h_{1}}=\frac{v-R}{u-R} \right )$

$or \;\;\;\;\;\frac{sin\theta _{1}}{sin\theta_{2}}=\frac{\mu _{2}}{\mu_{1}}\times \frac{h_{2}}{h_{1}}\;\;\;\;\;\left (\because \;\; \frac{sin\;i}{sin\;r}=\frac{\mu _{2}}{\mu _{1}} \right )$

$or \;\;\;\;\;\mu_{1}h_{1}sin\theta _{1}=\mu_{2}h_{2}sin\theta _{2}$

This is Abbe’s since condition.
This relation is valid for all the values of θ₁ and θ₂.
In this way a point N on axis imaged as N՛ on the axis by refraction from the surface XY.
A surface which does so, is known as aplanatic surface, and this surface is used in objectives of microscopes.
If aperture of the refracting surface is very small, then θ₁ and θ₂ will be very small.

∴ sin θ₁ ≈ tan θ₁ and sin θ₂ ≈ tan θ₂

and µ₁h₁ tan θ₁ = µ₂h₂ tan θ₂

This is Lagrange’s equation.
Also if the values of θ₁ and θ₂ are very small, then tan θ₁ ≈ θ₁ and tan θ₂ ≈ θ₂

µ₁h₁ θ₁ = µ₂h₂ θ₂

This is Helmholtz equation.

To know about Abbe’s sine condition in more detail click here.

Leave a Reply Cancel reply

Related Stories

Surface tension

Nuclear Physics

RPSC First Grade Physics-2

You may have missed

Surface tension

bharat ka bhugol

Senior teacher Maths test series

Om Sanatan