Chromatic aberration and its reduction
Aberration
- The spherical surfaces and lenses are used to create the images of given objects.
- If we find the position, size and forms of images by using simple equations, then there will be several defects or aberration in images.
- The defects in images formed by a lens or combination of lenses are known as aberration.

Chromatic aberration or Colour defect
- When white light incident on a prism, then after refraction form the prism it splits into seven colours.
- In the same way if white light incident on a lens and after refraction from the lens, we get the images of different colours, then such defect of lens is known as chromatic aberration or colour defect.
- Because a lens can be assumed as a combination of several prisms, and their angle of refraction decreases as we go from centre to the corner.
Reason
- The refractive index of lens material is different for different colours or the light of different wavelengths.
- The light of different wavelengths focuses at different and forms the image at different positions.
- From Cauchy relation µ = A + B/λ2
∵ λR > λV ⇒ µR < µV
∵ f ∝ 1/µ ⇒ fR > fV
- Since the focal length of red is highest, so the deviation of red is minimum and the deviation of violet is maximum.
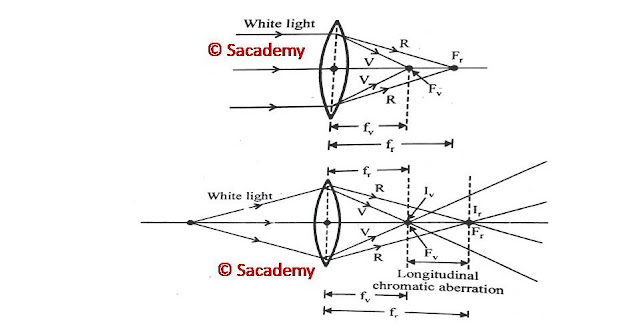
- (fr ー fv) measures the axial or longitudinal chromatic aberration.
Longitudinal chromatic aberration
- The difference of focal length of lens for red and violet colour provides the measure of axial or longitudinal chromatic aberration.
- Since focal length of lens
- But dispersive power of lens material is ω , so
- If fy = focal length of mean colour, then fy² = fv fr
- fr − fv = ωfy
- Thus longitudinal chromatic aberration is the product of dispersive power and focal length of ray of mean colour.
Transverse chromatic aberration
- If a white light object is placed normal to the axis of a lens then it is imaged normal to the axis.
- Since the refractive index of lens is different for different colours and hence the image formed normal to the axis will be of different colours and of different sizes.
- If I = size of image, O = size of object, u = distance of object from the optical centre of lens and v = distance of image from the optical centre of lens, then
- Magnification m = I/O = v/u
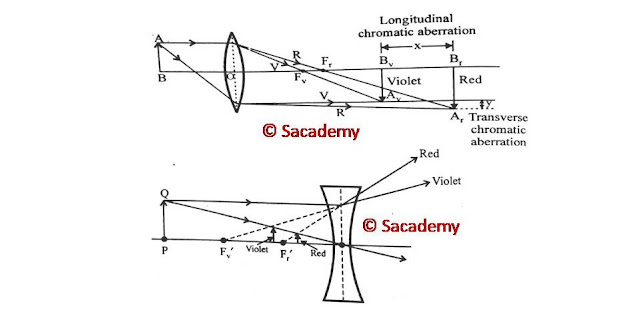
Here
- AB = White object
- AvBv = Violet colour image of given white object
- ArBr = Red colour image of given white object
- ArBr ー AvBv = Measure of transverse chromatic aberration
- Mr ー Mv = Transverse chromatic aberration in terms of magnification
- If the size of red image is greater than the size of violet image (Mr > Mv), then the transverse chromatic aberration is said to be positive (aberration due to convex lens).
- If Mr < Mv, then the transverse chromatic aberration is said to be negative (aberration due to concave lens).
Analytically
- The rate of change of size of image with respect to the wavelength is chromatic aberration.
- If x = axial distance, and y = transverse distance, then
- Longitudinal chromatic aberration = dx/dλ
- Transverse chromatic aberration = dy/dλ
Achromatic lens or Achromatism
- The process of minimizing chromatic aberration is known as achromatism.
- There are two methods for getting achromatism
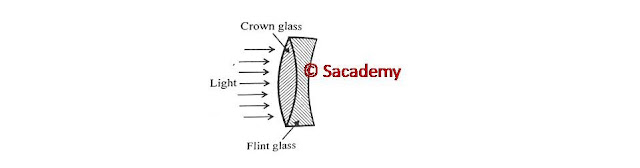
- By an achromatic doublet in which two lenses convex (crown glass) and concave (flint glass) are placed in contact.
- By placing two convex lenses of same material at a suitable distance.
Achromatic combination of two lenses in contact
- The combination of two or more lenses are arranged in such a way that the image obtained from it is free from chromatic aberration is achromatic lens.
- For convex lens fv < fr and for concave lens fv > fr
- Chromatic aberration of convex lens is positive.
- Chromatic aberration of concave lens is negative.
- To obtain the image free from chromatic aberration, the two lenses (one is convex and another is concave) are grouped together. Such arrangement is known as achromatic doublet.
- For achromatic doublet, we use a crown glass of high power (or low focal length) and a flint glass of low power (or large focal length).
- The focal length of two lenses are so adjusted that the focus of violet coincides with the focus of red.
- Since focal length of thin lens is
- Let f1 and f2 be the focal length of crown and flint glass respectively, then the focal length of combination will be
- For achromatism F = constant ⇒ dF = 0
- Since ω1 / ω2 = ー f1 / f2
- And ω1 and ω2 both are positive, so f1 and f2 must be of opposite sign. It means if one lens is convex, the other lens must be concave.
- If ω1 = ω2, then
- 1/ f1 + 1/f2 = 0 ⇒ 1/F = 0 ⇒ F = ∞
- Thus combination behaves as a plane glass plate, not as a lens. So the material should be different so that ω1 ≠ ω2
- If the combination behaves like a convergent lens, then power of convex lens should be greater than the power of concave lens or f1 < f2 hence ω1 < ω2 and therefore the convex lens should be of crown and concave lens should be of flint glass.
- The condition which we use here is only for the elimination of longitudinal chromatic aberration, transverse chromatic aberration can not be removed by it.
- If a number of lenses are combined to form achromatic lens, then
- ω1 / f1 + ω2 / f2 + ω3 / f3 + …= 0 or Σ (ω / f ) = 0
Achromatic combination of two lenses separated by a distance

- If two lenses are separated by a distance d, then the focal length of combination will be
- Since focal length depends on wavelengths
- For achromatism F = constant
- If both lenses are made up of same material, ω1 = ω2 = ω, then
- d = (f1 + f2) / 2
- Since this relation does not contain ω, so the combination has the same value for all the colours.
- Since d never be negative, so (f1 + f2) > 0, hence both the lenses must be either convex or the one with greater focal length must be convex.
To know about chromatic aberration and its reduction in detail in English click here and click here for bilingual lecture (Hindi/English).


