Liquid helium as a Boson system
- Ordinary helium consists almost entirely of neutral atom of the isotope 2He4.
- Since the total angular momentum of these atom is zero, so it follow the Bose-Einstein statistics.
Properties of helium at low temperature
- The helium gas at atmospheric pressure condenses at 4.3K temperature into a liquid helium having critical temperature 5.2K, and the density of this liquid helium is very low (ρ = 0.124 g/cm3).
- On further cooling the helium to about 0.82K, it does not freeze, and the liquid helium remains into liquid state up to absolute zero temperature i.e., T = 0K.
- It means the helium does not solidified at atmospheric pressure. To get the solid state of helium, it is subjected to an external pressure of at least 23 atm.
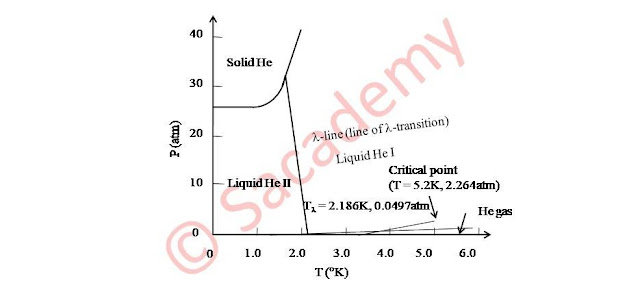
Phase transition of liquid He
- For He4 in liquid phase, there is another phase transition (λ-transition), which divides the liquid state into two phases HeI and HeII.
- While liquefying He at about 2.2K, density become an abrupt maximum and then decreases slightly.
- Therefore the critical temperature is at 2.186K and it represents a transition to a new state of matter, known as liquid HeII.
- In liquid HeII
- Heat conductivity is very large (order of 3 x 106 times greater).
- Coefficient of viscosity is gradually decreases with decrease in temperature and approaching to zero at absolute zero temperature.
- The specific heat curve is discontinuous at 2.186K and the shape of this curve is same as letter λ, and therefore this particular transition is known as λ-transition.
- The discontinuity temperature 2.186K is called λ-point.

- Since experimentally at λ-point, liquid HeII state has no latent heat so Keeson concluded that transition HeI → HeII at Tλ is a second order transition and as the pressure increases, the temperature decreases.
- Below the λ-line, liquid can be described by the two-fluid model.
- It behaves as if it consists of two components:
- A normal component, which behaves like a normal fluid.
- A super-fluid component with zero viscosity and zero entropy.
- The ratio of the respective densities (ρn / ρ) and (ρs / ρ) depend on the temperatures.
- Here ρn (ρs) is the density of normal (super-fluid) component, and ρ is the total density.
- By lowering the temperature, the fraction of the super-fluid density increases from 0 at Tλ to 1 at 0K.
- Below 1K, the He is almost completely super-fluid.
- Since ρn + ρs is constant, so it is impossible to create density waves of the normal component (and hence of the super-fluid component), which is similar to ordinary sound waves.
- This effect is known as second sound.

Explanation based on Bose-Einstein condensation model
London’s theory
- The behaviour of liquid He at low temperature is based on B-E statistics.
- London suggested that HeII is similar to B.E. gas and its λ-transition is the counter part of Bose-Einstein condensation in the ideal gas.
- In Bose-Einstein gas, degeneracy 1/D = (n/gsV) (2πmkT/h2)-3/2
- Since the helium atoms are light enough and the density (n/V) of the liquid is sufficiently high for the R.H.S. to be large and degeneracy to be small, but it is low enough for the liquid to behave as a gas.
- London concluded this λ-transition as a result of B.E. condensation and gave a similarity between λ-point and B.E. temperature T0.
- gs = (Zt)T = T0 = n / F3/2(0)
- Where translational partition function Zt = (2πmkT / h2)3/2 V
- ∴ gs (2πmkT0 / h2)3/2 V = n / 2.612, where T0 = (h2/2πmk) (n / 2.612Vgs)2/3
- For a gram molecule of helium in liquid state, V = 27.4 cm3, T0 = 3.12K.
- It is close to Tλ = 2.186K for the λ-point.
- This agreement between T0 and Tλ favours the London explanation.
- The decrease in entropy below Tλ being zero at 0.5K is explained by B.E. condensation because at T = T0 most of the particles rapidly fall into the ground state, which is characterized by zero entropy.
To know in detail about liquid helium click here.


