Phase velocity and Group velocity

Phase velocity (Wave velocity)

If a single monochromatic wave (wave of single frequency or wavelength) travels through a medium, then the velocity through which it propagate is wave velocity.
Equation of plane progressive wave propagating in x-direction

y = a sin (ωt – kx)

Here a = amplitude, ω = angular frequency, and k = 2π / λ = wave vector or propagation constant
Since in wave motion, the particles of the medium vibrates about their mean position continuously, the velocity acquired by particle during this motion is particle velocity.
During this motion, the disturbance (crest or trough) also produced and they also move in the direction in which the wave propagate and also with the same velocity.
The velocity of the disturbance through which it advances through the medium is phase velocity (wave velocity).

∵ v = νλ

Also k = 2π / λ and ω = 2πν

$\therefore \;\;\;\;\;v=\frac{\omega }{2\pi}\times \frac{2\pi}{k}$

$or \;\;\;\;\;v=\frac{\omega }{k}$

Above equation gives the wave velocity.
Thus the ratio of angular frequency to the propagation constant (wave vector) is known as wave velocity.
In equation y = a sin (ωt – kx), (ωt – kx) is phase of wave motion
For the planes of constant phase or wavefront

(ωt – kx) = constant

$\therefore \;\;\;\;\;\omega - k \frac{dx}{dt}=0$

$or \;\;\;\;\;\frac{dx}{dt}=\frac{\omega}{k}$

Above expression represents the wave velocity.
Since the wave velocity is the velocity with which planes of constant phase advance through the medium, and above expression is obtained for such type of wave, so it is also known as phase velocity.

$v_{p}=\frac{dx}{dt}=\frac{\omega }{k}$

Group velocity

In practical life we come across pulse or group of wave of slightly different frequencies. This group of waves are wave packets.
A wave packet refers to the case where two or more waves exist simultaneously.
The group velocity of a wave packet is the velocity with which the maximum amplitudes of the group advances in the medium.
This is the velocity with which the energy in the group is transmitted.
The group velocity is defined as the rate of change of angular velocity with respect to wave vector.

$v_{g}=\frac{d\omega}{dk}$

Let a wave packet is made up of two harmonic waves

y₁ = a sin (ωt – kx)

and y₂ = a sin [(ω + Δω) t – (k + Δk) x]

Let on superposition, these waves form a wave packet, then resultant displacement of wave packet

y = y₁ + y₂

$or\;\;\;\;\;y=2asin \left\{ \frac{(2\omega + \Delta \omega)t-(2k + \Delta k)x}{2} \right\}cos \left\{ \frac{(\Delta \omega)t-(\Delta k)x}{2} \right\}$

∵ Δω << ω and Δk << k

$\therefore \;\;\;\;\;y=2a cos \left\{ \frac{\Delta \omega}{2}t-\frac{\Delta k}{2}x \right\}sin (\omega t - kx)$

The amplitude of this equation is modulated by

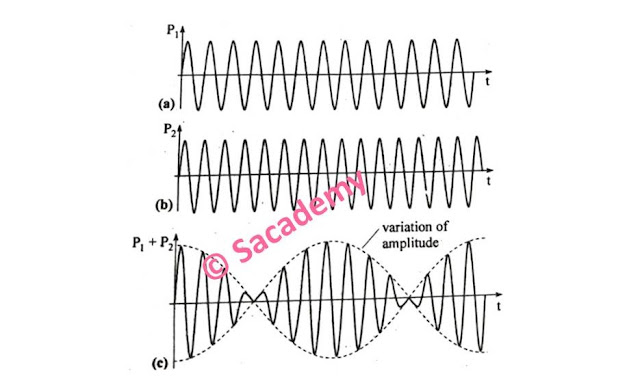
$2a cos \left\{ \frac{\Delta \omega}{2}t-\frac{\Delta k}{2}x \right\}$

Here figure (a) and (b) shows the two waves of slightly different frequencies, and figure (c) shows the resultant wave of these two waves.

$v_{g}=\frac{\Delta \omega}{\Delta k}$

If △ω and △k are very small then

$v_{g}=\displaystyle \lim_{\Delta k \to 0}\frac{\Delta \omega}{\Delta k}$

$or\;\;\;\;\;v_{g}=\frac{d\omega}{dk}$

Relation between phase velocity and group velocity

∵ ω = kv_p

Here ω = angular frequency, k = wave vector and v_p = phase velocity.

$v_{g}=\frac{d\omega }{dk}=\frac{d}{dk}(kv_{p})$

$or\;\;\;\;\;v_{g}=v_{p}+k\frac{dv_{p}}{dk}$

$But\;\;\;\;\;k=\frac{2\pi}{\lambda}\;\;\;\Rightarrow \;\;\;dk=-\frac{2\pi}{\lambda^{2}}d\lambda$

$\therefore \;\;\;\;\;v_{g}=v_{p}+\frac{2\pi}{\lambda}\frac{dv_{p}}{(-2\pi /\lambda^{2})d\lambda}$

$or \;\;\;\;\;v_{g}=v_{p}-\lambda \frac{dv_{p}}{d\lambda}$

This is the relation between phase velocity and group velocity.

Dispersive and non-dispersive medium

Non-dispersive medium

Here v_p = constant

∴ dv_p/dλ = 0

$But \;\;\;\;\;v_{g}=v_{p}-\lambda \frac{dv_{p}}{d\lambda}$

∴ v_g= v_p

Thus in non-dispersive medium, the waves of different frequencies move with the same phase and group velocity.
Example : Propagation of sound waves in gases.

Dispersive medium

Here dv_p/dλ > 0

$But \;\;\;\;\;v_{g}=v_{p}-\lambda \frac{dv_{p}}{d\lambda}$

∴ v_g< v_p

Thus in normal dispersion, the group velocity of wave is less than the phase velocity.
Example : Propagation of electromagnetic wave in any refractive medium.