कला वेग तथा समूह वेग (Phase velocity and Group velocity)

कला वेग (तरंग वेग)

यदि एक एकवर्णीय तरंग (एकल आवृत्ति या तरंग दैर्ध्य की तरंग) किसी माध्यम में से गुजरती है, तो वह वेग जिससे तरंग संचरित होती है, तरंग वेग कहलाता है।
x-दिशा में संचरित होनी वाली समतल प्रगामी तरंग का समीकरण

y = a sin (ωt – kx)

यहां a = आयाम, ω = कोणीय आवृत्ति तथा k = 2π / λ तरंग सदिश या संचरण नियतांक है।
चूंकि तरंग गति में माध्यम के कण माध्य स्थिति के परितः सतत् रूप से कम्पन्न करते हैं, इस गति के दौरान कणों द्वारा ग्रहण किया गया वेग, कण वेग कहलाता है।
इस गति के दौरान, विक्षोभ (शृंग तथा गर्त) भी उत्पन्न होते हैं तथा ये भी तरंग संचरण की दिषा में समान वेग से गति करते हैं।
विक्षोभ जिस वेग से माध्यम में आगे बढ़ते हैं वह वेग कला वेग (तरंग वेग) कहलाता है।

∵ v = νλ

साथ ही k = 2π / λ तथा ω = 2πν

$\therefore \;\;\;\;\;v=\frac{\omega }{2\pi}\times \frac{2\pi}{k}$

$or \;\;\;\;\;v=\frac{\omega }{k}$

उपरोक्त समीकरण तरंग वेग प्रदान करती है।
अतः कोणीय आवृत्ति तथा संचरण नियतांक (तरंग सदिश) का अनुपात तरंग वेग कहलाता है।
समीकरण y = a sin (ωt – kx) में (ωt – kx) तरंग गति की कला हैं।
नियत कला या तरंगाग्र वाले तल के लिए

(ωt – kx) = नियत

$\therefore \;\;\;\;\;\omega - k \frac{dx}{dt}=0$

$or \;\;\;\;\;\frac{dx}{dt}=\frac{\omega}{k}$

उपरोक्त समीरणक तरंग वेग दर्शाती है।
चूंकि तरंग वेग वह वेग है जिसके साथ नियत कला के तल आगे बढ़ते हैं, और इस प्रकार की तरंग के लिए उपरोक्त समीकरण प्राप्त की गई है, इसलिए कला वेग भी कहते हैं।

$v_{p}=\frac{dx}{dt}=\frac{\omega }{k}$

समूह वेग

वास्तवित जीवन में हम स्पंद या कुछ भिन्न आवृत्तियों के समूह के सम्पर्क में आते हैं। इन तरंगों का समूह, तरंग पैकेट कहलाता है।
तरंग पैकेट वह है, जिसमें दो या दो से अधिक तरंगें एक साथ स्थित होती हैं।
किसी तरंग पैकेट का समूह वेग वह वेग है, जिस वेग से समूह का अधिकतम आयाम माध्यम में आगे बढ़ता है।
यह वह वेग है, जिससे समूह में ऊर्जा पारगमित होती है।
तरंग सदिश के सापेक्ष कोणीय वेग में परिवर्तन की दर समूह वेग कहलाती है।

$v_{g}=\frac{d\omega}{dk}$

माना एक तरंग पैकेट दो आवर्ती तरंगों से निर्मित है।

y₁ = a sin (ωt – kx)

and y₂ = a sin [(ω + Δω) t – (k + Δk) x]

माना अध्यारोपण पर ये तरंगें, तरंग पैकेट का निर्माण करती हैं, तो तरंग पैकेट का परिणामी विस्थापन

y = y₁ + y₂

$or\;\;\;\;\;y=2asin \left\{ \frac{(2\omega + \Delta \omega)t-(2k + \Delta k)x}{2} \right\}cos \left\{ \frac{(\Delta \omega)t-(\Delta k)x}{2} \right\}$

∵ Δω << ω and Δk << k

$\therefore \;\;\;\;\;y=2a cos \left\{ \frac{\Delta \omega}{2}t-\frac{\Delta k}{2}x \right\}sin (\omega t - kx)$

इस समीकरण का आयाम निम्न से मॉडुलित होता है

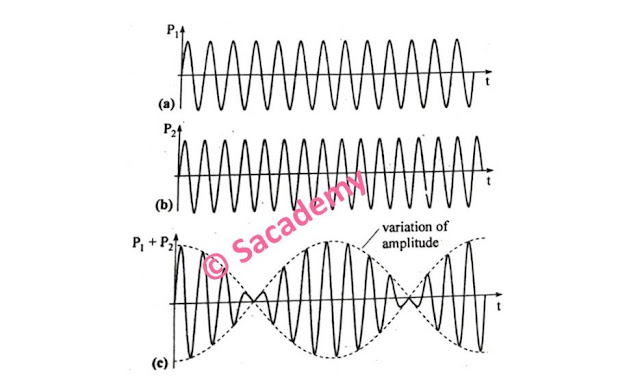
$2a cos \left\{ \frac{\Delta \omega}{2}t-\frac{\Delta k}{2}x \right\}$

यहां (a) तथा (b) दो तरंगों को दर्शाते हैं, जिनकी आवृत्तियों में बहुत कम अन्तर होता है, तथा (c) इन दोनों तरंगों के अध्यारोपण से प्राप्त परिणामी तरंग है।

$v_{g}=\frac{\Delta \omega}{\Delta k}$