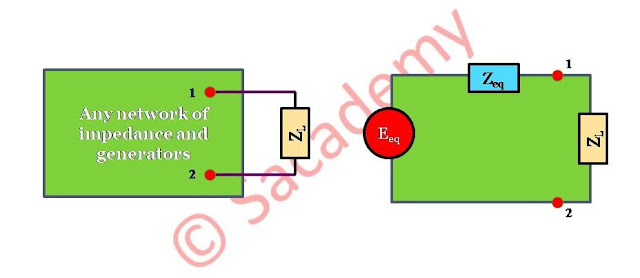
Thevenin’s Theorem
- According to Thevenin’s theorem any two terminal linear network containing linear impedances and one or more generators can be replaced with an equivalent circuit consisting of an equivalent impedance (Zeq) in series with an equivalent source of e.m.f. (Eeq).
- Eeq = e.m.f. between two terminals, when the external load is removed or when the circuit is open.
- Zeq = impedance at the output terminals, when all the sources of the e.m.f. are short circuited or replaced by their internal impedances.
Proof
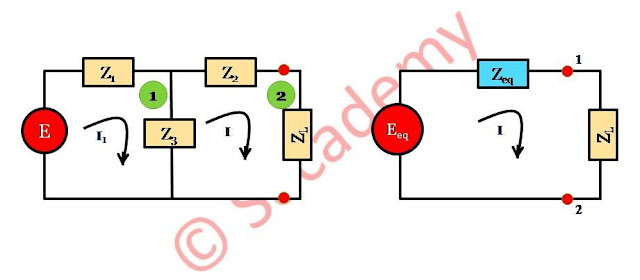
- Applying KVL in loop (1), E = I1 (Z1 + Z3) – IZ3
- Applying KVL in loop (2), 0 = I (Z3 + Z2 + ZL) – I1Z3 ⇒ I = [Z3 / (Z2 + Z3 + ZL)] I1
Since I = [Z3 / (Z2 + Z3 + ZL)] I1
Determination of Eeq
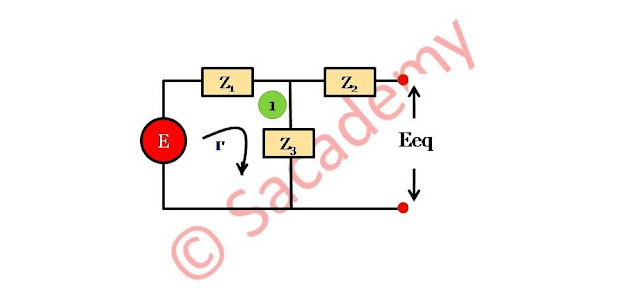
- Applying KVL in loop (1)
- E = I’ (Z1 + Z3) ⇒ I’ = E / (Z1 + Z3)
- Open circuit voltage, Eeq = I’Z3 ⇒ Eeq = E Z3/(Z1 + Z3)
Determination of Zeq

- Zeq = Z2 + {Z1Z3 / (Z1 + Z3)}
- Since Eeq = EZ3/(Z1 + Z3) and I = [E {Z3 / (Z1 + Z3)} / [ZL + {Z2 + Z1Z3 / (Z1 + Z3)}]
- ∴ I = Eeq / (ZL + Zeq)

- This is Thevenin’s equivalent circuit.
- By applying KVL in this loop we get
- Eeq = I (Zeq + ZL) ⇒ I = Eeq / (Zeq + ZL)
- Since the equations shown in red colour are same, hence Thevenin’s theorem is varied.
To know more about Thevenin’s theorem please click here.


