थेवेनिन प्रमेय
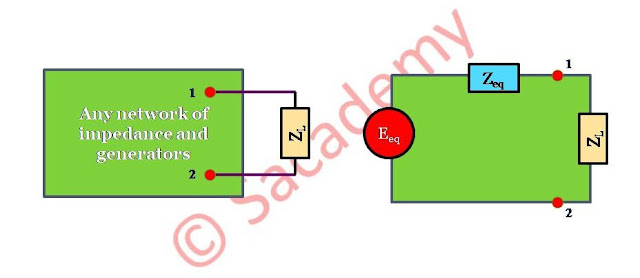
- इस प्रमेय के अनुसार किसी भी दो टर्मिनल रेखीय परिपथ, जिसमें कई प्रतिबाधाएं हों तथा एक या अधिक जनित्र हों, को एक तुल्य परिपथ, जिसका एक तुल्य विद्युत वाहक बल का स्रोत (Eeq) हो तथा जिसके श्रेणी क्रम में एक तुल्य प्रतिबाधा (Zeq) जुड़ी हो, से प्रतिस्थापित किया जा सकता है।
- Eeq = दो टर्मिनलों के मध्य वि.वा.बल का मान है, जब इसके बाह्य भार को या तो हटा दिया जाता है, या जब बाह्य परिपथ खुला हो।
- Zeq = बाह्य परिपथ के अनुदिश प्रतिबाधा का मान है, जब वि.वा.बल के सभी स्रोतों को या तो लघुपथित कर दिया जाता है, या उनको उनकी आन्तरिक प्रतिबाधाओं से प्रतिस्थापित कर दिया जाता है।
Proof
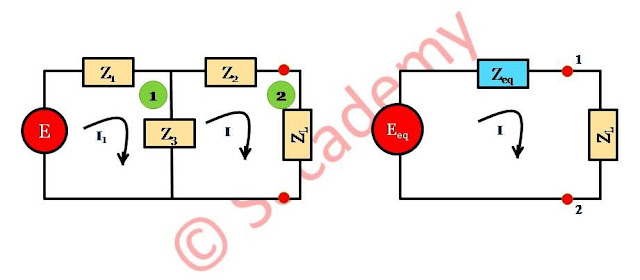
- लूप (1) में किरचॉफ वोल्टता नियम से, E = I1 (Z1 + Z3) – IZ3
- लूप (2) में किरचॉफ वोल्टता नियम से, 0 = I (Z3 + Z2 + ZL) – I1Z3 ⇒ I = [Z3 / (Z2 + Z3 + ZL)] I1
चूंकि I = [Z3 / (Z2 + Z3 + ZL)] I1
Eeq का मान ज्ञात करना
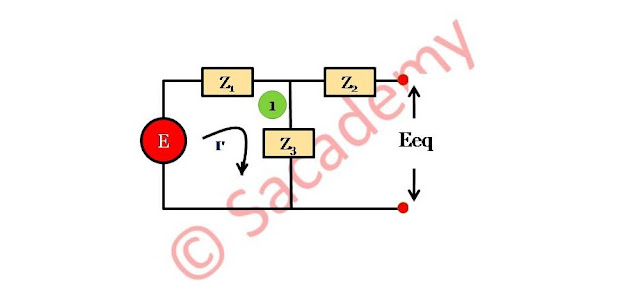
- लूप (1) में किरचॉफ वोल्टता नियम से
- E = I’ (Z1 + Z3) ⇒ I’ = E / (Z1 + Z3)
- खुले परिपथ की वोल्टता, Eeq = I’Z3 ⇒ Eeq = E Z3/(Z1 + Z3)
Zeq का मान ज्ञात करना

- Zeq = Z2 + {Z1Z3 / (Z1 + Z3)}
- चूंकि Eeq = EZ3/(Z1 + Z3) and I = [E {Z3 / (Z1 + Z3)} / [ZL + {Z2 + Z1Z3 / (Z1 + Z3)}]
- ∴ I = Eeq / (ZL + Zeq)

- यह थेवेनिन तुल्य परिपथ है।
- इस लूप में किरचॉफ के वोल्टता नियम से
- Eeq = I (Zeq + ZL) ⇒ I = Eeq / (Zeq + ZL)
- चूंकि लाल रंग में दिखाई गई दोनों समीकरणें समान हैं, अतः थेवेनिन प्रमेय सिद्ध होती है।
थेवेनिन प्रमेय के बारे में अधिक विस्तार से जानने के लिए यहां क्लिक करें।


