मोटा लेन्स तथा इसके प्रधान बिन्दु
मोटा लेन्स
- दो गोलीय सतहों का संयोजन मोटा लेन्स कहलाता है, यदि उनके ध्रुवों के मध्य की दूरी उनकी वक्रता त्रिज्याओं की तुलना में नगण्य नहीं होती है।
- इसे दो पतले लेन्सों के संयोजन के रूप में माना जा सकता है।
- इन लेन्सों की मोटाई उनकी फोकस दूरियों की तुलनीय होती है।
मोटे लेन्स के प्रधान बिन्दु
- माना µ लेन्स के पदार्थ का अपवर्तनांक है।
- t लेन्स की मोटाई है।
- R1 तथा R2 दिए गए लेन्स की क्रमशः प्रथम तथा द्वितीय वक्रता त्रिज्याएं हैं।
- F1 तथा F2 क्रमशः प्रथम तथा द्वितीय फोकस बिन्दु हैं।
- H1 तथा H2 क्रमशः प्रथम तथा द्वितीय मुख्य बिन्दु हैं।
- f1 तथा f2 दिए गए मोटे लेन्स की क्रमशः प्रथम तथा द्वितीय फोकस दूरियां हैं।
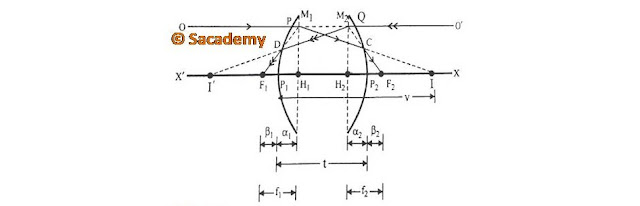
मोटे लेन्स के प्रधान बिन्दु
तुल्य फोकस दूरी
- यदि मोटे लेन्स के दोनों ओर समान माध्यम हों, तो
- H1F1 = f1 = – f , तथा H2F2 = f2 = f
सतह PP1 द्वारा अपवर्तन
∵ u = ∞, v = P1I, μ1 = 1, μ2 = μ तथा R = R1
सतह QP2 द्वारा अपवर्तन
- इस समय I बिम्ब की तरह कार्य करता है तथा अन्तिम प्रतिबिम्ब F2 पर प्राप्त होता है।
यहां u = P2I, v = P2F2, μ2 = 1, μ1 = μ तथा R = R2
- ΔM2H2F2 तथा ΔCP2F2 से
- ΔPP1I तथा ΔCP2I से
- उपरोक्त दो समीकरणों से
∵ P2I = P1I − P1P2 = P1I − t
- पतले लेन्स के लिए t → 0, तथा f → f0
मोटे लेन्स की शक्ति
द्वितीय फोकस बिन्दु की स्थिति (P2F2 = β2)
- द्वितीय फोकस बिन्दु की दूरी द्वितीय अपवर्तक सतह के ध्रुव से नापी जाती है।
द्वितीय मुख्य बिन्दु की स्थिति (P2H2 = α2)
- द्वितीय मुख्य बिन्दु की दूरी द्वितीय अपवर्तक सतह के ध्रुव से नापी जाती है।
∵ P2H2 = H2F2 − P2F2
∴ α2 = P2H2 = f − β2
चिन्ह परिपाटी के उपयोग से, उपरोक्त समीकरण का रूप निम्न होगा
प्रथम फोकस बिन्दु की स्थिति (P2F1 = β1)
- इसके लिए माना लेन्स निकाय पर किरण दायीं ओर से अर्थात् O՛Q की ओर से आपतित होती है एवं इस अवस्था में प्रतिबिम्ब F1 पर बनता है। इसलिए β2 में R1 को -R2 से तथा f को -f से प्रतिस्थापित करते हैं।
प्रथम मुख्य बिन्दु की स्थिति (P1H1 = α1)
- इसके लिए हम R1 → –R2 तथा f → – f का प्रयोग द्वितीय मुख्य बिन्दु की स्थिति α2 में करते हैं।
- मोटे लेन्स तथा मोटे लेन्स के प्रधान बिन्दुओं के बारे में और अधिक जानने के लिए यहां क्लिक करें।


